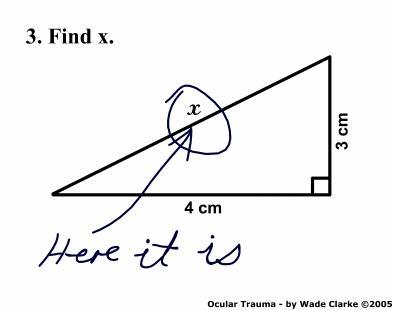
donde el pensamiento lateral se traduce en pensamiento literal. Donde el pensamiento "tradicional" hubiese leído "halle el valor de x", usando el teorema de Pitágoras, el pensamiento lateral, probablemente espoleado por no recordar el susodicho teorema, e incluso por no saber lo que significa "teorema" o lo que son los "catetos" (sin chisteeeees...) o la "hipotenusa", lee literalmente la pregunta... y halla la x como si de un "Dónde está Wally" se tratase. Ahí, encima de la hipotenusa. Y, aún no sabiendo lo que es una hipotenusa, se puede recurrir al lenguaje gráfico, y todos felices.Todos menos el alumno listillo que contestase eso, claro, que sin duda acabó suspendido. Porque, mis queridos niños, mis queridas niñas y mis adorados helados de piña, pese a lo que pueda parecer leyendo cosas por ahí, el pensamiento lateral no vale para todo y no es cierto que teniendo la capacidad de pensamiento lateral ya lo tengas todo resuelto. El pensamiento lateral, ténganlo todos en cuenta, no sirve para aprobar exámenes de matemáticas, como se puede comprobar en estos ejercicios (sacados del imprescindible y enciclopédico blog Curioso Pero Inútil, que ya tardan en visitar a la voz de ya). Todos han ido de laterales, y todos suspendidos, por listillos.
Hombreyacontantatonteríapordios...
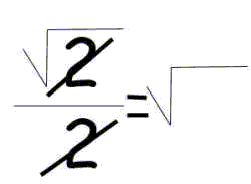
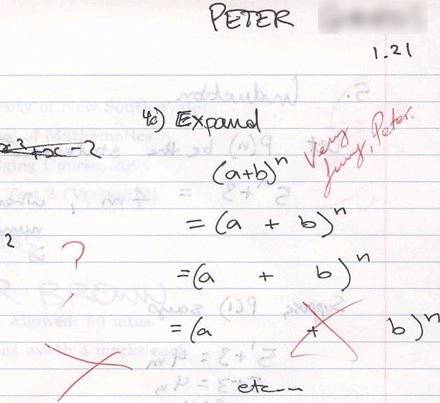
Por cierto, nótese que los ejemplos son sajones, están todos en inglés. La LOGSE esa que se ve que es tan mala y la culpable de todos los males de la humanidad no ha tenido nada que ver...
5 comentarios:
Ay, qué gracia xD. Son el tipo de ejemplos que el profesor de matemáticas del instituto ponía a principio de curso para mostrar lo que eran las "matemágicas"
Siempre es mejor cuando lo hace un profesor y no un alumno, como uno que tuve en Teleco. Frases como:
"Si el transistor no conduce... le
pegamos hasta que conduzca"
y
"Los electrones se mueven y tienen su masa y, atención que ahora vienen las emociones fuertes, los huecos que dejan los electrones también se mueven y tienen masa".
Norda, pues tu profesor se equivocaba. Esas cosas lo que son es un ejemplo de lo que pasa cuando aplicas la lógica a algo que, por su propia definición (y pese a lo que digan los profesores de matemáticas) no la tiene. Las matemáticas son un lenguaje, no otra cosa, y, como tal, la única lógica que tienen es la etimológica. Y aún esta es una lógica totalmente arbitraria
Urui, tengo la electrónica muuuuy oxidada, pero si no recuerdo mal, un transistor no conduce... hasta que le arreas un zurriagazo de potencial superior a su fractura dieléctrica y pasa a conducir de golpe. Así que tu profesor no decía ninguna tontería. Y lo segundo es estrictamente cierto... en función de dónde pongas los ejes de coordenadas. Y como cuando trabajas con electrones, en realidad lo que estás haciendo es trabajar con agujeros, porque todas las ecuaciones están definidas del revés, pues lo lógico es disponer el sistema de referencia con huecos móviles y con masa, y luego, si procede, hacer la transformada. Es correcto.
Eh... no. El profe se refería a golpearlo físicamente con algo parecido a un martillo.
Ains, me gustaba la física de semiconductores, aquello de considerar "tiempo infinito" a un par de milisegundos tenía su encanto.
Ah, vale. Eso es lo que los químicos llamamos el "método científico". Con las teles suele funcionar...
Publicar un comentario